Franck & Hertz forsøget
Øvelsens formål
Det er øvelsens formål direkte at eftervise eksistensen af energiniveauer i
atomet.
Teori
Der benyttes en triode med en enatomig gas (Hg-damp) ved et tryk af størrelsesordenen
0,1 torr.
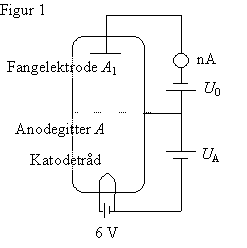 Elektronerne
fra glødetråden K accelereres af potentialforskellen UA
mellem K og en gitterformet anode A. Afstanden fra K til A
er adskillige gange større end elektronernes middelvejlængde. Efter passagen
af gitteret (anoden) løber elektronerne op mod en potentialforskel U0
mellem A og en fangelektrode A1, også kaldet en
modelektrode. Kun de elektroner, der ankommer til gitteret med kinetisk energi
større end e·U0, bidrager til strømmen gennem røret
og dermed til strømstyrken, I, som måles med et følsomt amperemeter.
Afstanden fra A til A1 er lille i forhold til
elektronernes frie middelvejlængde i Hg-dampen, hvorfor de kun sjældent
støder sammen med Hg-atomerne på denne strækning. Det viser sig, at
hvis UA ikke er alt for stor, så ankommer hovedparten af
elektronerne til gitteret med samme hastighed, som hvis røret havde været
lufttomt, selv om elektronerne på strækningen fra K til A må være
stødt sammen med Hg-atomer. Disse sammenstød må have været »elastiske«.
Da et Hg-atom er mange gange tungere end en elektron, mister elektronen
ikke energi ved sammenstødet.
Elektronerne
fra glødetråden K accelereres af potentialforskellen UA
mellem K og en gitterformet anode A. Afstanden fra K til A
er adskillige gange større end elektronernes middelvejlængde. Efter passagen
af gitteret (anoden) løber elektronerne op mod en potentialforskel U0
mellem A og en fangelektrode A1, også kaldet en
modelektrode. Kun de elektroner, der ankommer til gitteret med kinetisk energi
større end e·U0, bidrager til strømmen gennem røret
og dermed til strømstyrken, I, som måles med et følsomt amperemeter.
Afstanden fra A til A1 er lille i forhold til
elektronernes frie middelvejlængde i Hg-dampen, hvorfor de kun sjældent
støder sammen med Hg-atomerne på denne strækning. Det viser sig, at
hvis UA ikke er alt for stor, så ankommer hovedparten af
elektronerne til gitteret med samme hastighed, som hvis røret havde været
lufttomt, selv om elektronerne på strækningen fra K til A må være
stødt sammen med Hg-atomer. Disse sammenstød må have været »elastiske«.
Da et Hg-atom er mange gange tungere end en elektron, mister elektronen
ikke energi ved sammenstødet.
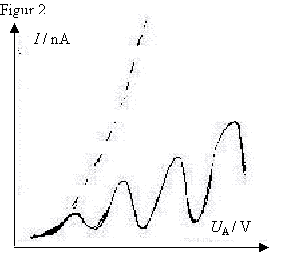 Hvis
røret havde været lufttomt, ville man forvente en (UA-I)
graf som vist stiplet på figur 2. Men når røret indeholder Hg-damp,
kommer grafen til at se ud som den fuldt optrukne kurve. Det første fald i strømmen
forklares på følgende måde: Når en elektron har tilstrækkelig energi til at
anslå et Hg-atom fra grundtilstanden til 1. exciterede tilstand, vil den
hermed miste så meget energi, at den ikke kan overvinde modspændingen og nå
hen til fangelektroden. Strømstyrken begynder derfor at aftage, når
elektronerne har tilstrækkelig energi til at anslå et Hg-atom. Det næste
fald i strømstyrken sker, når elektronerne får energi nok til at anslå 2
Hg-atomer osv. Forskellen i energi mellem grundtilstanden og 1. exciterede
tilstand er for Hg 4,89 eV. Derfor sker der et fald i strømstyrken hver gang
accelerationsspændingen stiger med 4,89 V. Afstanden mellem to nabotoppe er altså
4,89 V. Når de exciterede Hg-atomer spontant falder tilbage til
grundtilstanden udsendes fotoner. Disse er i det ultraviolette område og kan
derfor ikke ses. De kan dog registreres i Hg spektret med en ultravioletfølsom
detektor og derved kan ovenstående fortolkning af Franck-Hertz forsøget
bekræftes - eller hvis vi vil kan vi sige, at Franck-Hertz forsøget
bekræfter Bohrs teori for fotonemission.
Hvis
røret havde været lufttomt, ville man forvente en (UA-I)
graf som vist stiplet på figur 2. Men når røret indeholder Hg-damp,
kommer grafen til at se ud som den fuldt optrukne kurve. Det første fald i strømmen
forklares på følgende måde: Når en elektron har tilstrækkelig energi til at
anslå et Hg-atom fra grundtilstanden til 1. exciterede tilstand, vil den
hermed miste så meget energi, at den ikke kan overvinde modspændingen og nå
hen til fangelektroden. Strømstyrken begynder derfor at aftage, når
elektronerne har tilstrækkelig energi til at anslå et Hg-atom. Det næste
fald i strømstyrken sker, når elektronerne får energi nok til at anslå 2
Hg-atomer osv. Forskellen i energi mellem grundtilstanden og 1. exciterede
tilstand er for Hg 4,89 eV. Derfor sker der et fald i strømstyrken hver gang
accelerationsspændingen stiger med 4,89 V. Afstanden mellem to nabotoppe er altså
4,89 V. Når de exciterede Hg-atomer spontant falder tilbage til
grundtilstanden udsendes fotoner. Disse er i det ultraviolette område og kan
derfor ikke ses. De kan dog registreres i Hg spektret med en ultravioletfølsom
detektor og derved kan ovenstående fortolkning af Franck-Hertz forsøget
bekræftes - eller hvis vi vil kan vi sige, at Franck-Hertz forsøget
bekræfter Bohrs teori for fotonemission.
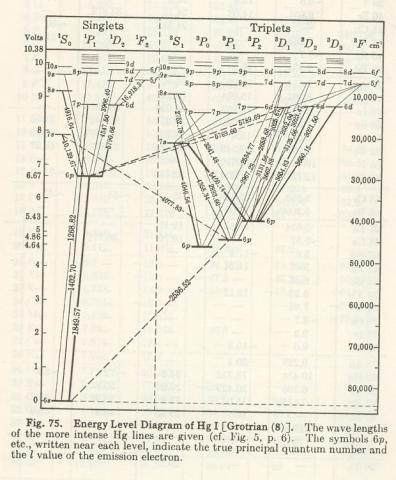
Opgave: Udregn frekvens og bølgelængde for de udsendte fotoner.
Identificer overgangen på diagrammet til højre.
Forsøgsopstilling
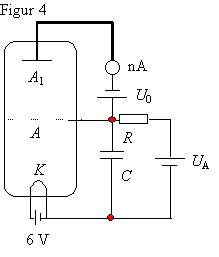 Apparatet består af et særligt udformet rør med Hg-damp. Røret er
anbragt i en termostatstyret varmeovn. Temperaturen måles. Den bør være
ca. 180°C . Da strømstyrken I er af størrelsesorden 10-9
A, er fangelektroden højisoleret fra det øvrige rør med et specielt
keramisk
materiale. Der benyttes korte ledninger til forbindelsen til
amperemeteret. Glødetråden tilsluttes 6 V vekselspænding. Accelerationsspændingen
tilsluttes via et RC-led (f.eks. R = 1 MW
og C = 50m F). Man opnår herved en forsinkelse som gør, at metrene kan følge
med og hurtige spændingsændringer udglattes.
Apparatet består af et særligt udformet rør med Hg-damp. Røret er
anbragt i en termostatstyret varmeovn. Temperaturen måles. Den bør være
ca. 180°C . Da strømstyrken I er af størrelsesorden 10-9
A, er fangelektroden højisoleret fra det øvrige rør med et specielt
keramisk
materiale. Der benyttes korte ledninger til forbindelsen til
amperemeteret. Glødetråden tilsluttes 6 V vekselspænding. Accelerationsspændingen
tilsluttes via et RC-led (f.eks. R = 1 MW
og C = 50m F). Man opnår herved en forsinkelse som gør, at metrene kan følge
med og hurtige spændingsændringer udglattes.
Forsøgets udførelse
Straks ved forsøgets begyndelse tændes for varmeovnen. Apparaterne stilles
op som vist på figur 4. Bemærk, at elementet på 1,5 V er koblet modsat
accelerationsspændingen. Med et voltmeter med autorange måles
accelerationsspændingen
fra K til A, som er lig med spændingen over kondensatoren. Strømstyrken måles
ved at tilslutte et voltmeter til
amperemetrets analoge udgang.
I Datalyse vælges måling på 2 apparater. Sæt tid pr måling til 0,5
sekund og antallet af målinger til 1000. Start måling og skru op for spændingen.
Stop måling når/hvis der fås OL på amperemetret.
Udregn strømstyrken i tabellen og gem tabellen.
Tegn (UA, I)-graf.
Bestem alle maksima ved at klikke på max-knappen i panelet til venstre. Tegn
en ny graf, hvor de målte spændinger afbildes som funktion af deres numre.
Bestem ionisationsenergien vha. denne graf.
Gentag forsøget indtil der forhåbentlig er opnået et pænt resultat.
Eksempel på Graf fra Datalyse
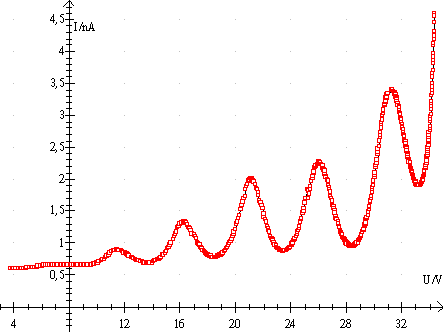
 Elektronerne
fra glødetråden K accelereres af potentialforskellen UA
mellem K og en gitterformet anode A. Afstanden fra K til A
er adskillige gange større end elektronernes middelvejlængde. Efter passagen
af gitteret (anoden) løber elektronerne op mod en potentialforskel U0
mellem A og en fangelektrode A1, også kaldet en
modelektrode. Kun de elektroner, der ankommer til gitteret med kinetisk energi
større end e·U0, bidrager til strømmen gennem røret
og dermed til strømstyrken, I, som måles med et følsomt amperemeter.
Afstanden fra A til A1 er lille i forhold til
elektronernes frie middelvejlængde i Hg-dampen, hvorfor de kun sjældent
støder sammen med Hg-atomerne på denne strækning. Det viser sig, at
hvis UA ikke er alt for stor, så ankommer hovedparten af
elektronerne til gitteret med samme hastighed, som hvis røret havde været
lufttomt, selv om elektronerne på strækningen fra K til A må være
stødt sammen med Hg-atomer. Disse sammenstød må have været »elastiske«.
Da et Hg-atom er mange gange tungere end en elektron, mister elektronen
ikke energi ved sammenstødet.
Elektronerne
fra glødetråden K accelereres af potentialforskellen UA
mellem K og en gitterformet anode A. Afstanden fra K til A
er adskillige gange større end elektronernes middelvejlængde. Efter passagen
af gitteret (anoden) løber elektronerne op mod en potentialforskel U0
mellem A og en fangelektrode A1, også kaldet en
modelektrode. Kun de elektroner, der ankommer til gitteret med kinetisk energi
større end e·U0, bidrager til strømmen gennem røret
og dermed til strømstyrken, I, som måles med et følsomt amperemeter.
Afstanden fra A til A1 er lille i forhold til
elektronernes frie middelvejlængde i Hg-dampen, hvorfor de kun sjældent
støder sammen med Hg-atomerne på denne strækning. Det viser sig, at
hvis UA ikke er alt for stor, så ankommer hovedparten af
elektronerne til gitteret med samme hastighed, som hvis røret havde været
lufttomt, selv om elektronerne på strækningen fra K til A må være
stødt sammen med Hg-atomer. Disse sammenstød må have været »elastiske«.
Da et Hg-atom er mange gange tungere end en elektron, mister elektronen
ikke energi ved sammenstødet. Hvis
røret havde været lufttomt, ville man forvente en (UA-I)
graf som vist stiplet på figur 2. Men når røret indeholder Hg-damp,
kommer grafen til at se ud som den fuldt optrukne kurve. Det første fald i strømmen
forklares på følgende måde: Når en elektron har tilstrækkelig energi til at
anslå et Hg-atom fra grundtilstanden til 1. exciterede tilstand, vil den
hermed miste så meget energi, at den ikke kan overvinde modspændingen og nå
hen til fangelektroden. Strømstyrken begynder derfor at aftage, når
elektronerne har tilstrækkelig energi til at anslå et Hg-atom. Det næste
fald i strømstyrken sker, når elektronerne får energi nok til at anslå 2
Hg-atomer osv. Forskellen i energi mellem grundtilstanden og 1. exciterede
tilstand er for Hg 4,89 eV. Derfor sker der et fald i strømstyrken hver gang
accelerationsspændingen stiger med 4,89 V. Afstanden mellem to nabotoppe er altså
4,89 V. Når de exciterede Hg-atomer spontant falder tilbage til
grundtilstanden udsendes fotoner. Disse er i det ultraviolette område og kan
derfor ikke ses. De kan dog registreres i Hg spektret med en ultravioletfølsom
detektor og derved kan ovenstående fortolkning af Franck-Hertz forsøget
bekræftes - eller hvis vi vil kan vi sige, at Franck-Hertz forsøget
bekræfter Bohrs teori for fotonemission.
Hvis
røret havde været lufttomt, ville man forvente en (UA-I)
graf som vist stiplet på figur 2. Men når røret indeholder Hg-damp,
kommer grafen til at se ud som den fuldt optrukne kurve. Det første fald i strømmen
forklares på følgende måde: Når en elektron har tilstrækkelig energi til at
anslå et Hg-atom fra grundtilstanden til 1. exciterede tilstand, vil den
hermed miste så meget energi, at den ikke kan overvinde modspændingen og nå
hen til fangelektroden. Strømstyrken begynder derfor at aftage, når
elektronerne har tilstrækkelig energi til at anslå et Hg-atom. Det næste
fald i strømstyrken sker, når elektronerne får energi nok til at anslå 2
Hg-atomer osv. Forskellen i energi mellem grundtilstanden og 1. exciterede
tilstand er for Hg 4,89 eV. Derfor sker der et fald i strømstyrken hver gang
accelerationsspændingen stiger med 4,89 V. Afstanden mellem to nabotoppe er altså
4,89 V. Når de exciterede Hg-atomer spontant falder tilbage til
grundtilstanden udsendes fotoner. Disse er i det ultraviolette område og kan
derfor ikke ses. De kan dog registreres i Hg spektret med en ultravioletfølsom
detektor og derved kan ovenstående fortolkning af Franck-Hertz forsøget
bekræftes - eller hvis vi vil kan vi sige, at Franck-Hertz forsøget
bekræfter Bohrs teori for fotonemission.
 Apparatet består af et særligt udformet rør med Hg-damp. Røret er
anbragt i en termostatstyret varmeovn. Temperaturen måles. Den bør være
ca. 180°C . Da strømstyrken I er af størrelsesorden 10-9
A, er fangelektroden højisoleret fra det øvrige rør med et specielt
keramisk
materiale. Der benyttes korte ledninger til forbindelsen til
amperemeteret. Glødetråden tilsluttes 6 V vekselspænding. Accelerationsspændingen
tilsluttes via et RC-led (f.eks. R = 1 M
Apparatet består af et særligt udformet rør med Hg-damp. Røret er
anbragt i en termostatstyret varmeovn. Temperaturen måles. Den bør være
ca. 180°C . Da strømstyrken I er af størrelsesorden 10-9
A, er fangelektroden højisoleret fra det øvrige rør med et specielt
keramisk
materiale. Der benyttes korte ledninger til forbindelsen til
amperemeteret. Glødetråden tilsluttes 6 V vekselspænding. Accelerationsspændingen
tilsluttes via et RC-led (f.eks. R = 1 M