Stefan-Boltzmanns lov

Den udstrålede effekt fra et absolut sort legeme med overfladeareal A og den absolutte temperatur T er givet ved:

     Pstråling = A·s·T 4, 

hvor Stefan-Boltzmanns konstant, s = 5,67·10-8W·m-2·K-4

Formålet med forsøget er at eftervise Stefan-Boltzmanns lov.

Apparatur

Der benyttes en Stefan-Boltzmanns lampe, et voltmeter, et amperemeter , en skydemodstand  og et termometer. Lampen må højst tilsluttes en spænding på 13 volt. Datalyse kan benyttes sammen med to multimetre med interface. Vælg dataopsamling fra to apparater i Datalyse og vælg retur for hver måling. Når strømstyrker og spædninger er målt og resistansen af lampen er beregnet, udregnes temperaturen af glødetråden.  
Funktionen er T = 287,15·(R/R300)0,88454·e5,0E-6·(R/R300) er en god tilnærmelse. Dvs. et produkt af en potensfunktion og en eksponentiel udvikling. Bemærk, at R/R300 ændres pga ændring og resistivitet og længde.

Forsøg 1

Bestemmelse af resistansten, Rref ved stuetemperatur:

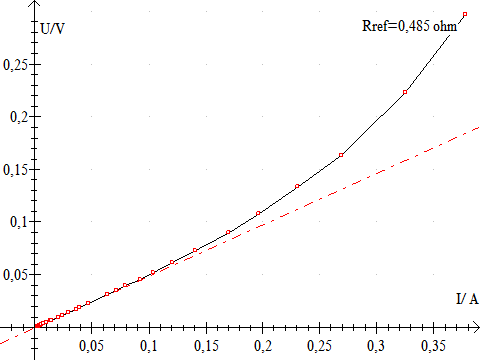
Udfør en række målinger af U og I ved så små strømstyrker, at man kan se bort fra temperaturstigningen i pæren. Det vil være tilfældet, hvis spændingerne vælges i området 1 mV til 10 mV. Udregn herefter resistansen ved stuetemperatur vha. Ohms lov, som vist på grafen. Mål samtidigt temperaturen i lokalet, tstue.

Rref og tstue benyttes til at beregne resistansen R300 ved temperaturen T = 300 K. R300 beregnes vha. formlen for resistansen som funktion af temperaturen:

     R = R0(1 +a·DT), 

hvor R0 er resistansen ved 0° C og a er temperaturkoefficienten og DT er temperaturstigningen. Wolframs temperaturkoefficient er 0,0048 1/K ved 273 K. 

Udregningen foregår i to omgange:

  1. udregning af R0 vha  Rref = R0(1 +a·tstue),
  2. udregning af R300 vha. R300 = R0(1 +a·(300 K - 273,15 K)),

Forsøg 2

Lav en serie målinger af spænding U og strømstyrke I. Lav ca. Ti målinger i området 10-100 mV, og ti målinger i området 100-1000 mV og ti målinger i området 1-13 V. For at få kunne indstille spændingen præcis for små spændinger kan man indsætte en 100 ohms modstand i serie med lampen eller man kan bruge en spændingsdeler. Alle værdier skrives i den samme tabel.

 

Behandling af måleresultater

Hvis man har benyttet Datalyse til dataopsamling kan udregningerne foretages i tabellen i Datalyse ellers kan de laves i Excel. Her er et klip fra en tabel i Datalyse:

t/s

I/ A

U/V

P/W

R/ohm

R/R300

T/K

Pst/W

Ptab/W

143,593

0,359

0,294

0,105

0,819

1,668

442,6

0,016

0,089

 

 

 

 

 

 

 

 

 

  1. Beregn varmeeffekten P

  2. R beregnes vha. Ohms lov.

  3. R/R300 beregnes, idet R300 er i forsøg 1.

  4. Temperaturen T beregnes vha. den tilnærmede funktion, som er beskrevet ovenfor. 

Herefter afbildes effekten P, som funktion af temperaturen T.

Grafen viser, at effekten P stiger med temperaturen, men hvordan? Dobbeltlogaritmisk afbildning. Ved høje temperaturer, ses det, at effekten stiger proportionalt med T 3,74, men …

Ved lave temperaturer sker varmetransporten hovedsageligt ved varmeledning og strømning. Varmeeffekten bør derfor være proportional med temperaturforskellen mellem glødetråden og omgivelserne. Ved høje temperaturer sker varmetransporten hovedsageligt ved stråling. Dvs. 

     P = Pledning + Pstråling = a1·(T - Tstue) + a2·T 4

Hvor stor en del af effekten P, der skyldes varmeledning og hvor stor en del, der skyldes varmestråling, kan bestemmes ved fitning i Datalyse. Benyt et funktionsudtryk af formen

      f(t) = a1*1E-3*(T - Tstue) + a2*1E-12*T 4.

Eksempel på fit i Datalyse

Denne graf viser, at P = 0,574·10-3W/K·(T-Tstue) + 0,418·10-12W/K·T 4.

Vi kan nu afbilde både P, Pledning og Pstråling som funktion af T:

P: sort graf. Pstråling: blå graf. Pledning: rød graf. Ved lave temperaturer dominerer Pledning og ved høje temperaturer dominerer Pstråling.

Benyt Stefan-Boltzmanns lov til at udregne arealet af glødetråden.